Will we ever run out of photographs?
As the web accumulates photos (another 6,037 posted to Flickr in the last minute…), and as projects like Photosynth start to infer intermediate perspectives between these images, one could conceive of collisions — multiple instances the same image, pixel for pixel, from two different authors.
Multi-megapixel full-color pixel images weighing in at dozens of megabytes distance us from what, exactly, these images are at the computationally atomic level of bits. Going back to the same concept on a smaller scale, makes the simplicity of the computational representation of an image clear. Black and white makes this exceedingly basic — an image can be as simple as a grid of 0s and 1s:
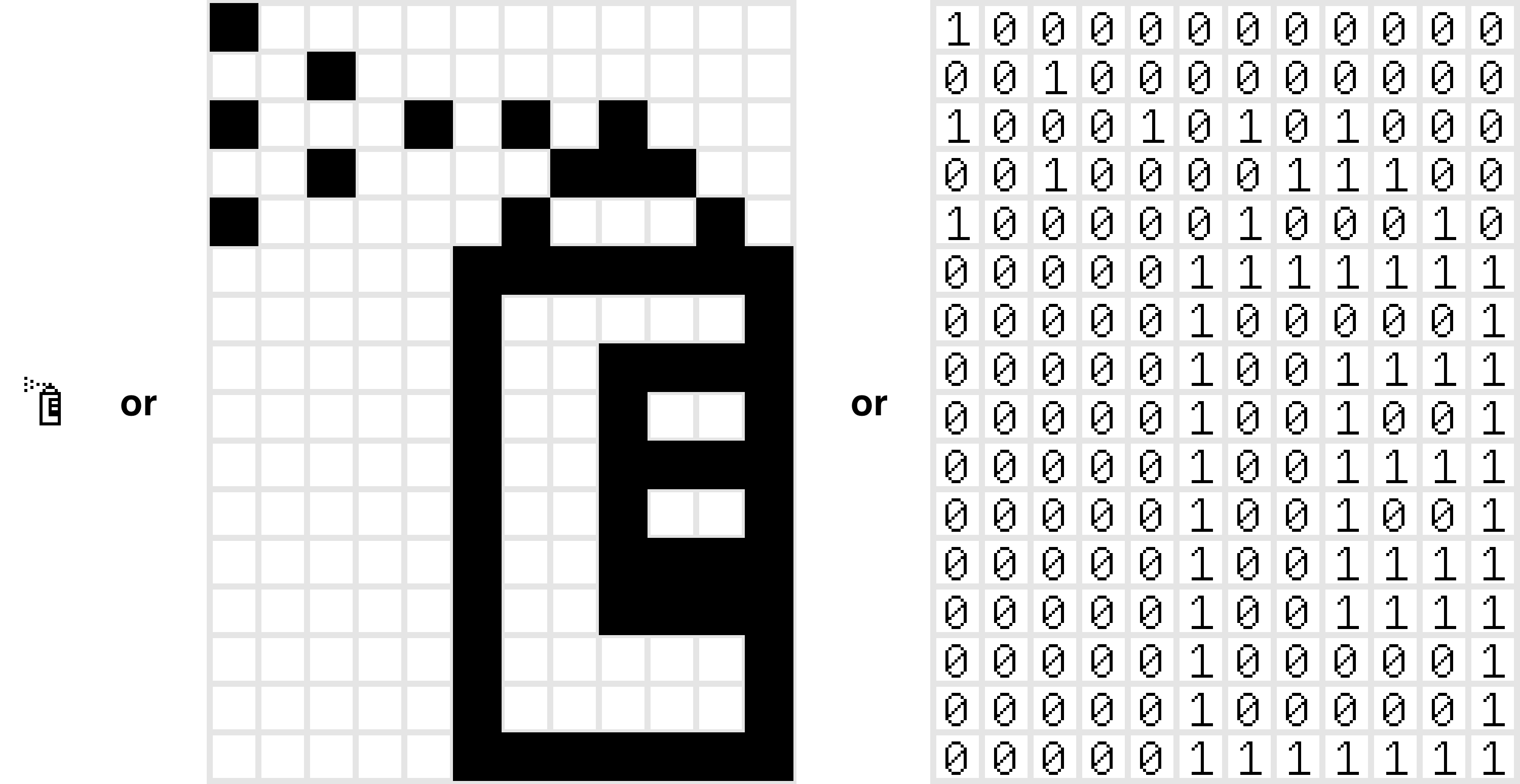
Ditch the grid, and you’re left with a big binary number:
100000000000001000000000100010101000001000011100100000100010000001111111000001000001000001001111000001001001000001001111000001001001000001001111000001001111000001000001000001000001000001111111
Convert that to base ten, and you have:
3,138,742,632,065,979,126,417,490,138,422,209,858,437,835,786,299,168,264,319
The picture’s just a number. It’s just one of the possible black and white images that could fit in the 12 x 16 pixel grid. In fact, it’s image number 3,138,742,632,065,979,126,417,490,138,422,209,858,437,835,786,299,168,264,319 out of 6,277,101,735,386,680,763,835,789,423,207,666,416,102,355,444,464,034,512,896 possible images.
Every single one of the ~6 octodecillion possible 1 bit 12 x 16 images could be generated computationally. We don’t need a camera, a photographer, or an icon artist — a simple program looping through and rendering each possibility would, eventually, stumble upon that exact spray can. And, eventually, it would run out of images to render, and the creative possibilities of a 12 x 16 pixel 1 bit canvas would be exhausted, or, at least, definitively explored.
These numbers are huge — incomprehensible. For all practical intents and purposes, these numbers are as good as infinity, and yet, they’re finite in every objective sense.
Scaling this idea up to the high-res color images typical of the web, the number gets even more ridiculous. You can find the number of possible distinct images for a given bit depth and resolution with the following formula:
Possible Photos = (2^Bit Depth)^(Width * Height)
This brings up a few questions.
First, this exposes an inherent and often unconsidered flaw of digital mediums — finite resolution means finite potential representations, suggesting a degree of determinism in digital systems.
Second, what might one discover by traversing the range of possible images with an algorithm instead of a computer? Would anything be discovered? Might we see glimpses of the future or past? By definition, these photographs would all have to be present in the set — portraits of every human, past and present, confidential texts, etc.
Third, what does this say about photographic creativity? Is creating a photo an act of genesis and original thought, or is the photographer merely colliding with an inevitable, preexisting combination of bits?
Fourth, exploring data sets like this also brings up the question: What’s the threshold of perception? How many pixels do we need to have before something representational emerges? Of course, deciding on any threshold implies compromise, and the representation of different facets of reality can move this threshold radically. For example, a single black pixel could be said to represent a dark room, and therefore could be said to hold some representational qualities. Representing text on a page or the nuances of a tree, however, would require thousands (maybe millions) of pixels.
A few artists explored this idea in the 90s: Jim Campbell’s The End (1996) John Simon’s Every Icon (1997)
It’s also worth considering that this concept is agnostic to the actual way in which in a particular bit string is interpreted. For any digital object of a particular size, this theory of finite possibilities can be applied and explored.
For example, artist Kyle McDonald explored this idea in sound, generating every possible sequence of the chromatic scale’s 12 notes: